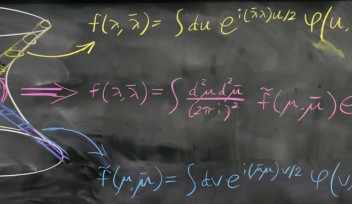ホログラフィーとツイスター理論を結びつける新たな数学

  一人の現代理論物理学者が、難題に立ち向かっています。

  物理学者のヤーシャ・ネイマン博士は「より多くを学べば学ぶほど、現実はますます捉えにくいものとなります。 絶対が相対になったり、静的なものが動的なものになったり、確実なものが不確実なものになってしまうのです。」 と、語ります。

  沖縄科学技術大学院大学の 量子重力ユニットを率いるネイマン准教授は、日々この難題に取り組んでいます。 ネイマン准教授の物理学における専門の一つである量子重力の分野では、空間と時間が湾曲するアインシュタインの現代重力理論を描く「一般相対性理論」と、原子および原子よりさらに小さな素粒子のスケールでの特性を表す量子力学を統一することを目指しています。 空間自体の幾何学構造が量子の不確定性の対象となってしまう場合、物理学者はどのように方程式を書くことができるのだろうか？ と問い続けるネイマン准教授によると、基本理論の今日のフロンティアとも言える量子重力は、それまでの概念よりもはるかに複雑であることが分かってきていると言います。

  「私たちの指の間でさえ空間が滑り現象を起こしているという概念があるので、私たちは宇宙の記述において足場にできる新たな基盤を模索するのです。」

量子重力についての難題に日々取り組むヤーシャ・ネイマン准教授

  代替となる基盤についての模索は、本質的には、現実を記述する新たな言語の模索とも言えます。これこそが、最近ネイマン准教授がJournal of High Energy Physics誌に発表した論文の主要テーマなのです。 この論文でネイマン准教授は、ホログラフィーやツイスター理論のような物理学で確立されたアプローチを土台にし、新境地への到達に向けた空間と時間の幾何学的な新たな視点を提示しています。

  ホログラフィーとは、1990年代後半に開発された、宇宙を構成する物質が1次元の物で構成されているという弦理論から派生したものです。ホログラフィーにおける描像は、宇宙の果ては、空間の境界を形成する無限大の球の表面です。 この球内において幾何学的な形状が変動しても、球の表面上の「無限大における境界」は固定されたままになります。

  過去20年間ホログラフィーは、量子重力の思考実験を行うための非常に貴重なツールでした。 しかし宇宙論的な観測から、このアプローチは実際のところ、私たちの世界には適用できないことがわかりました。

  「急速に拡大する宇宙と光速が有限であることが合わさり、宇宙観測はかなりの広大な領域をカバーはしているものの、現在もしくは将来において本来は可能であるはずの宇宙空間の観測は、限定的な領域となってしまっています」と、ネイマン准教授は説明します。

  このような世界では、宇宙のホログラフィー描像の基礎である無限遠における境界は、もはや物理的に意味をなさなくなってしまいます。 そうなると、宇宙に固定された表面を見つけようとするのではなく、宇宙空間そのものを全く考えない新たな枠組みが必要となります。

  1960年代、量子重力を理解するため、物理学者のロジャー・ペンローズはそのような根本的な代替案を提案しました。 ペンローズのツイスター理論では、幾何学的な点は、延伸した光線に最もよく似た形状のツイスターというものに置き換えられています。 このツイスター空間で、ペンローズは電磁気や重力のような光速で移動する「場」を表現する非常に効率的な方法を発見しました。 しかし現実は場だけからでは構成できません。すなわち、電荷間の電気力や、一般相対性理論のより複雑なケースにおける場のエネルギーに起因する重力など、様々な場の間の相互作用も考慮に入れる必要があるのです。 しかしこのような描像に、一般相対性理論の相互作用を含めることは、大変な作業であることが知られています。

２次元の光線としての時空における拡張エンティティ―であるツイスターを表現した図

『Spinors and Space-Time』R.　ペンローズ、W.　リンドラー共著、Cambridge Monographs on Mathematical Physics、Cambridge、Cambridge University Press.

  場との相互作用を完全に考慮した、本格的な量子重力理論を、ツイスター言語を用い、一般相対性理論より簡単に表現することはできるのでしょうか？ネイマン准教授は可能だと答えます。

  ネイマン准教授のモデルは、1980年代と90年代にロシアの物理学者、ミカエル・ヴァシリエフによって開発された高次スピン重力モデルに基づいています。 高次スピン重力モデルは弦理論の姉妹版のように考えられており、「一般相対性理論を再現するにはあまりにも単純ですが、アイデア構築の遊び場としては非常に役立つのですよ」とネイマン准教授は説明します。 特に、ホログラフィーとツイスター理論との間の橋渡しを模索するには、高次スピン重力モデルは最適だそうです。

  イゴール・クレバノフとアレクサンダー・ポリアコフは2001年に高次スピン重力モデルが弦理論と同様、ホログラフィーで記述することができることを発見しました。空間内のその振る舞いは、無限の世界における境界として完全に捉えることができるのです。一方、それらの方程式は、たとえこれらが通常空間における特定の点に結びつけられていたとしても、ツイスターのような変数を含むのです。

  こうした過去の研究をもとに、ネイマン准教授の論文では、ホログラフィーとツイスター理論の言語を結びつける数学的辞書を構築する付随的なステップを取り入れているのです。

  「このテーマのカギとなる根本の数学はすべて平方根なのです」と、ネイマン准教授は説明しています。 「それは回転や反射などの幾何学的操作の「半分」を行う捉えにくい方法を特定することなのです。 賢い平方根というものは、頑丈な壁の亀裂を見つけ、さらに壁を2つに切り開き 、新たな世界を見せてくれるものなのです 。」

  数学と物理学の歴史では、平方根が長い間このように使われてきました。 実際、電子やクォークのようなすべての素粒子の固有の形やツイスターは、空間の通常方向における平方根で表されます。 空間と無限遠における境界、ツイスター空間を結びつけるネイマン准教授の手法は、いわばある種の平方根を求める作業であると言えます。

  ネイマン准教授は、自身による概念の実証が、無限遠における境界に頼らずとも、量子重力論に向かう道を切り開くことができると期待しています。

  「世界の体系を明らかにするには、多くの創造性が必要です。そういう作業がまた楽しいのですけれどね」と、ネイマン准教授は語っています。